Decybele (dB) to logarytmiczna jednostka miary używana do pomiaru natężenia dźwięku, mocy i napięcia. Opiera się na skali logarytmicznej, co pozwala na łatwe porównywanie wartości w szerokim zakresie. Decybele są jednostką względną, zawsze wymagającą punktu odniesienia. Skala ta jest zgodna z prawem Webera-Fechnera, opisującym reakcję ludzkich zmysłów na bodźce.
Zastosowanie decybeli obejmuje akustykę, elektronikę i telekomunikację. Różnica 10 dB odpowiada dziesięciokrotnemu wzrostowi natężenia dźwięku. W praktyce, poziom hałasu 55 dB może powodować dyskomfort, a powyżej 75 dB jest szkodliwy dla zdrowia.
Najważniejsze informacje:- Decybele to jednostka względna, zawsze wymagająca punktu odniesienia
- Skala decybeli jest logarytmiczna, co ułatwia przedstawienie dużych zmian wartości
- Wzrost o 10 dB oznacza dziesięciokrotny wzrost natężenia dźwięku
- Decybele znajdują zastosowanie w akustyce, elektronice i telekomunikacji
- Poziom hałasu powyżej 75 dB jest szkodliwy dla zdrowia
Czym są decybele?
Decybele (dB) to logarytmiczna jednostka miary używana do określania stosunku dwóch wielkości, najczęściej w kontekście pomiaru dźwięku. Skala logarytmiczna dB pozwala na wygodne przedstawienie szerokiego zakresu wartości w sposób odpowiadający ludzkiej percepcji. Decybel jest jednostką względną, co oznacza, że zawsze potrzebuje punktu odniesienia.
Dla napięć, stosunek wyrażony w decybelach oblicza się według wzoru:
$$ k[dB] = 20 \log_{10} \left(\frac{U_2}{U_1}\right) $$Przykładowo, jeśli mamy dwa napięcia: U1 = 1V i U2 = 2V, to różnica między nimi wyniesie około 6 dB. To pokazuje, jak decybele pomiar dźwięku przekładają się na praktyczne obliczenia.
Skala logarytmiczna w pomiarach dźwięku
Skala logarytmiczna dB to sposób przedstawiania wartości, w którym każda jednostka odpowiada wielokrotności poprzedniej. W przypadku decybeli stosuje się logarytm o podstawie 10. Wykorzystanie tej skali w akustyce wynika z faktu, że ludzkie ucho reaguje na zmiany dźwięku w sposób nieliniowy.
Dzięki skali logarytmicznej dB możemy łatwo przedstawić ogromne różnice w poziomie natężenia dźwięku, które występują w naturze. Odpowiada to prawu Webera-Fechnera, które mówi, że percepcja bodźca jest proporcjonalna do logarytmu jego fizycznej intensywności. To prawo tłumaczy, dlaczego decybele pomiar dźwięku są tak skuteczne w opisywaniu naszych doznań słuchowych.
Zalety skali logarytmicznej w akustyce
- Umożliwia przedstawienie szerokiego zakresu wartości w przystępny sposób
- Odzwierciedla sposób, w jaki ludzkie ucho odbiera zmiany głośności
- Pozwala na łatwe porównywanie różnych poziomów dźwięku
- Upraszcza obliczenia związane z tłumieniem i wzmacnianiem sygnałów
Czytaj więcej: Jak pisać teksty piosenek: 5 niezawodnych kroków dla początkujących
Jak obliczać wartości w decybelach?
Dla mocy, stosunek wyrażony w decybelach oblicza się według wzoru:
$$ k[dB] = 10 \log_{10} \left(\frac{P_2}{P_1}\right) $$Gdzie P1 i P2 to porównywane wartości mocy. Ten wzór jest kluczowy dla zrozumienia, jak decybele skala logarytmiczna przekłada się na konkretne wartości.
Przykładowo, jeśli moc sygnału wzrośnie 100 razy, zmiana w decybelach wyniesie 10 * log10(100) = 20 dB. To pokazuje, jak duże zmiany mocy przekładają się na stosunkowo małe wartości w skali decybelowej.
Praktyczne zastosowanie obliczeń decybelowych
| Dziedzina | Zastosowanie |
|---|---|
| Akustyka | Pomiar głośności w decybelach |
| Elektronika | Ocena wzmocnienia sygnału |
| Telekomunikacja | Analiza tłumienia sygnału w kablach |
| Medycyna | Badanie słuchu |
| Przemysł | Kontrola hałasu maszyn |
Poziomy dźwięku w codziennym życiu
Głośność w decybelach otaczających nas dźwięków może się znacznie różnić. Znajomość typowych poziomów hałasu pomaga zrozumieć, jak decybele skala logarytmiczna przekłada się na nasze codzienne doświadczenia.
- Szept - 30 dB
- Normalna rozmowa - 60 dB
- Ruchliwa ulica - 70 dB
- Odkurzacz - 75 dB
- Kosiarka do trawy - 85 dB
- Koncert rockowy - 110 dB
- Startujący samolot odrzutowy - 130 dB
- Próg bólu - 140 dB
Zastosowanie decybeli poza akustyką
Jednostki logarytmiczne akustyka to nie jedyne zastosowanie decybeli. W elektronice decybele służą do pomiaru wzmocnienia sygnału w układach, takich jak wzmacniacze czy filtry. Pozwala to na łatwe porównywanie wydajności różnych komponentów.
W telekomunikacji decybele skala logarytmiczna jest używana do oceny tłumienia sygnału w kablach i łączach radiowych. Umożliwia to precyzyjne planowanie zasięgu sieci i jakości transmisji. Decybele znajdują też zastosowanie w optyce, sejsmologii czy nawet w ekonomii, wszędzie tam, gdzie potrzebne jest porównywanie wielkości o znacznie różniących się wartościach.
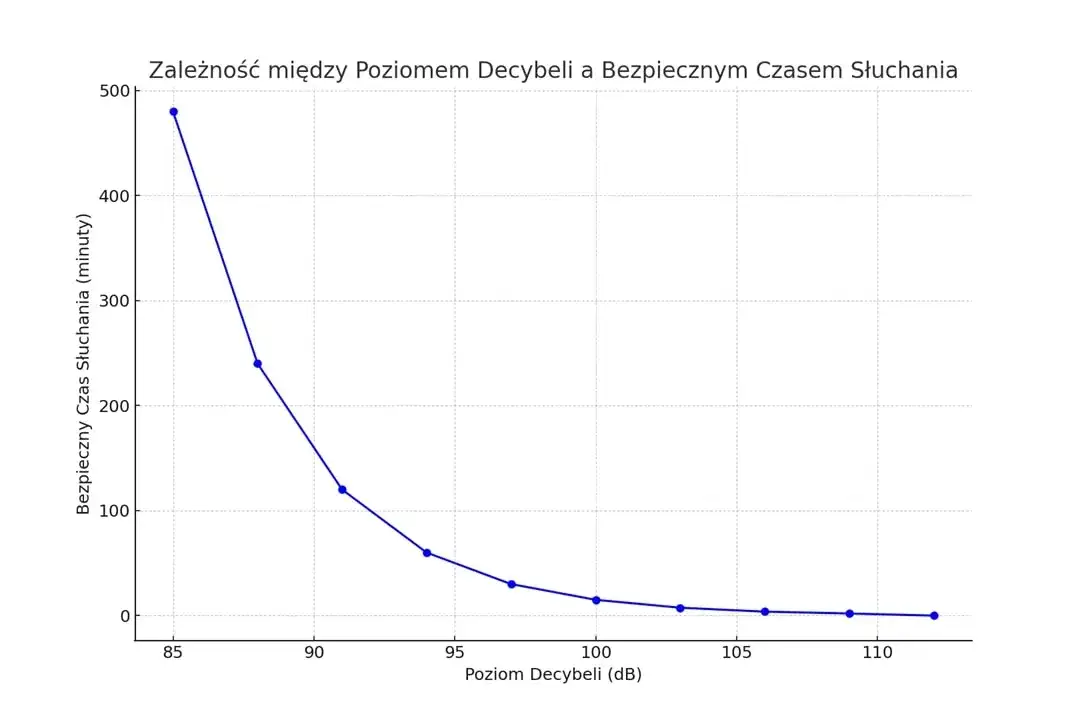
Wpływ poziomów dźwięku na zdrowie człowieka
Zrozumienie poziomu natężenia dźwięku jest kluczowe dla ochrony naszego zdrowia. Długotrwała ekspozycja na hałas może prowadzić do poważnych problemów zdrowotnych. Bezpieczny poziom dźwięku to generalnie poniżej 70 dB przez dłuższy czas.
Skutki długotrwałej ekspozycji na hałas mogą obejmować utratę słuchu, szumy uszne, problemy z koncentracją, a nawet choroby sercowo-naczyniowe. Dlatego tak ważne jest, aby rozumieć, jak decybele pomiar dźwięku przekłada się na nasze codzienne doświadczenia. Zaleca się stosowanie ochronników słuchu w hałaśliwych środowiskach i ograniczanie czasu ekspozycji na głośne dźwięki.
Normy hałasu w różnych środowiskach
| Środowisko | Dopuszczalny poziom hałasu (dB) |
|---|---|
| Biuro | 55-65 |
| Szkoła | 35-50 |
| Obszar przemysłowy | 70-75 |
| Strefa mieszkaniowa (dzień) | 55 |
| Strefa mieszkaniowa (noc) | 45 |
| Sala koncertowa | 80-90 |
Skala liniowa vs. logarytmiczna w pomiarach dźwięku
Różnica między skalą liniową a logarytmiczną jest kluczowa dla zrozumienia, dlaczego decybele skala logarytmiczna są tak powszechnie stosowane w akustyce. Skala liniowa reprezentuje wartości w równych odstępach, podczas gdy skala logarytmiczna kompresuje duże zakresy wartości. To sprawia, że skala logarytmiczna dB jest idealna do przedstawiania ogromnych różnic w intensywności dźwięku.
Zalety skali logarytmicznej w kontekście pomiaru dźwięku są ogromne. Pozwala ona na przedstawienie całego zakresu słyszalnych dźwięków w przystępny sposób, od najcichszych szmerów po ogłuszające huki.
Przykładowo, zmiana głośności z 10 dB na 20 dB na skali liniowej wyglądałaby jak mały skok, podczas gdy w rzeczywistości oznacza dziesięciokrotny wzrost intensywności dźwięku. Decybele pomiar dźwięku w skali logarytmicznej pozwalają na intuicyjne zrozumienie takich różnic.
Przyrządy do pomiaru poziomu dźwięku
Sonometr, znany też jako miernik poziomu dźwięku, to podstawowe narzędzie do pomiaru hałasu skala dB. To precyzyjne urządzenie, które przekształca ciśnienie akustyczne na odczyt elektryczny.
Zasada działania miernika poziomu dźwięku opiera się na wykorzystaniu mikrofonu do przechwytywania fal dźwiękowych. Sygnał jest następnie przetwarzany elektronicznie, aby odzwierciedlić sposób, w jaki ludzkie ucho reaguje na różne częstotliwości. Finalny odczyt jest prezentowany w decybelach, często z różnymi ważeniami częstotliwościowymi (np. dBA, dBC).
Inne urządzenia wykorzystywane w pomiarach akustycznych to analizatory widma, które rozkładają dźwięk na składowe częstotliwości, oraz dozymetry hałasu, mierzące skumulowaną ekspozycję na dźwięk w czasie. Te narzędzia pomagają lepiej zrozumieć, jak decybele skala logarytmiczna przekłada się na rzeczywiste warunki akustyczne.
Decybele: Klucz do zrozumienia dźwięku i jego wpływu na nasze życie
Decybele i skala logarytmiczna stanowią fundament nowoczesnej akustyki, umożliwiając precyzyjny pomiar hałasu i zrozumienie jego wpływu na nasze zdrowie. Dzięki tej jednostce możemy łatwo porównywać ogromne różnice w natężeniu dźwięku, od szeptu po huk startującego samolotu.
Znajomość poziomów natężenia dźwięku w decybelach pomaga nam lepiej dbać o nasz słuch i świadomie kształtować nasze otoczenie akustyczne. Pamiętajmy, że wzrost o zaledwie 10 dB oznacza podwojenie odczuwalnej głośności, co podkreśla wagę ochrony przed nadmiernym hałasem.
Zastosowanie decybeli wykracza daleko poza akustykę, obejmując elektronikę, telekomunikację i wiele innych dziedzin. Ta wszechstronność czyni z decybeli uniwersalne narzędzie do opisywania i analizy różnorodnych zjawisk, gdzie kluczowe jest porównywanie wartości o znacznie różniących się wielkościach.
